بازی آمار و احتمال و برنامه نویسی در کلاس دانشگاه

در جلسه اول کلاس آمار و احتمال استاد ابوالحسنی در دانشگاه بودیم و قرار شد بجای تدریس با هم بازی آمار و احتمال انجام بدیم و من سه مورد از موارد جالب رو که سناریو اونا رو با برنامه نویسی طراحی کردم، اینجا آوردم.

بازی اول، قضیه معروف تولدها

یک کلاس شامل 58 نفر را فرض کنید. به نظر شما احتمال اینکه دو نفر در این جمع وجود داشته باشند که دقیقا روز و ماه تولدشان یکسان باشد چقدر است؟ اگر شهودی بخواهید بگویید به نظر شما چگونه است؟ بیایید با هم این سناریو را در برنامه نویسی پیاده سازی کنیم:)
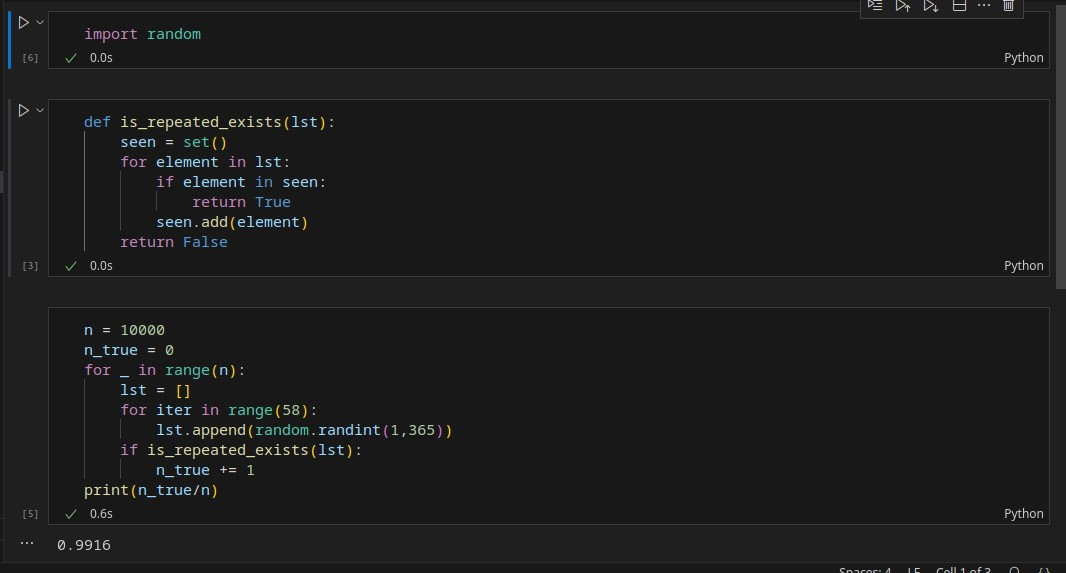
 برای اینکار 58 عدد تصادفی از 1 تا 365 انتخاب میکنیم و در داخل یک لیست قرار میدهیم؛ همچنین یک تابع پیاده سازی میکنم تا برسی کند که آیا دو مقدار برابر در لیست وجود دارد یا نه؛ و این کار را مثلا ده هزار بار تکرار میکنیم و تعداد دفعاتی که دو مقدار برابر (دو نفر با روز و ماه تولد یکسان) وجود دارد را بر تعداد کل دفعات(10000) تقسیم میکنیم؛ نتیجه اعجاب انگیز است! هر بار که برنامه را اجرا میکنید به عدد بیش از 99 درصد میرسید! بله بسیار عجیب است، اما کاملا ممکن است  و چیزی برخلاف شهود ما!
 استاد از این مورد تعبیر احتمال به فراوانی نسبی یاد کردند. 
تعداد کلاس حدود 30 نفر بود و استاد گفت روز و ماه تولد دو نفر از اعضای خانواده خود را بخاطر داشته باشید؛ به این صورت 90 نفر هستیم، و سپس به صورت رندم و تصادفی از یک دانشجو شروع کرد و پیش رفت و هر دانشجو با ذکر تاریخ تولد ها مشخص شد که خیلی سریع افرادی یافت میشوند که دقیقا روز و ماه تولد یکسان دارند! و این احتمال بسیار بالایی داشت، حتی استاد اول کلاس حاضر شد که با ما سر این موضوع شرط بندی کند:)

صفحه ویکی پدیای مسئله تاریخ تولد

بازی دوم، مسابقه پسر-قهرمان و پسر-پدر

فرض کنید پدر و پسر و یک قهرمان داریم؛ پسر قرار است با پدر و قهرمان سه ست مسابقه دهد؛ طبیعتا احتمال برد قهرمان از پسر بیشتر است نسبت به برد پدر از پسر؛  دو مدل برای مسابقه داریم:
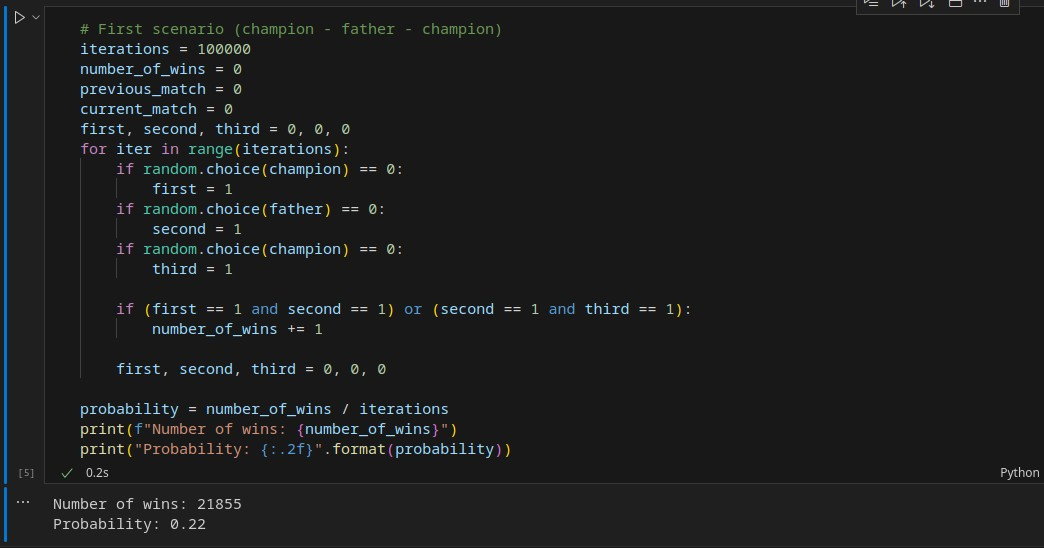
1) قهرمان – پدر – قهرمان
یعنی اول با قهرمان مسابقه دهد، سپس با پدر و مجددا با قهرمان

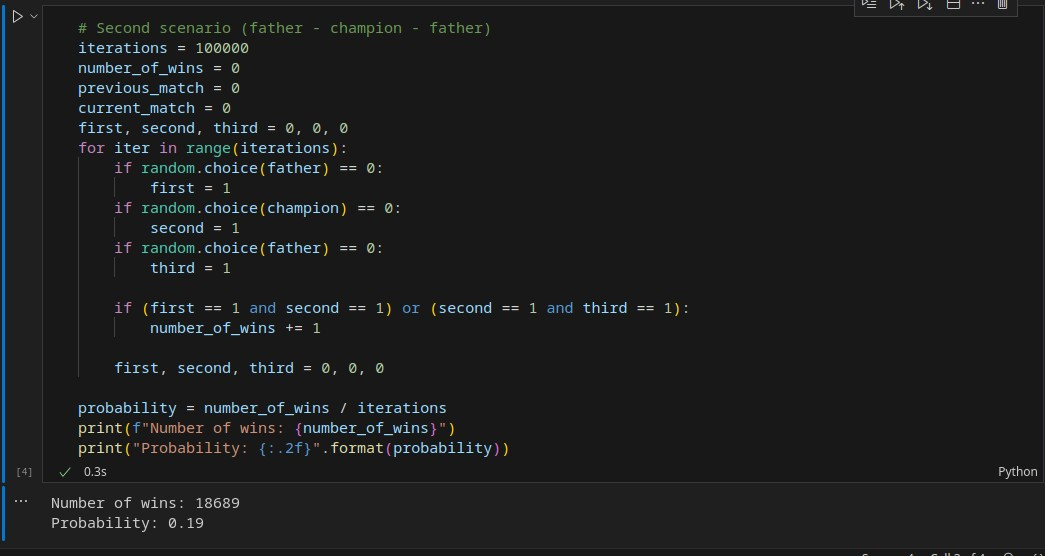
2) پدر – قهرمان – پدر
یعنی اول با پدر مسابقه دهد، سپس با قهرمان و مجددا با پدر

به نظر شما در کدام مدل بیشتر احتمال دارد که پسر دو مسابقه پشت سر هم را برنده شود؟
یعنی فرضا در حالت 1 در دو مسابقه اول با پدر و قهرمان برنده شود یا اینکه در دو مسابقه دوم با قهرمان و پدر
 شهودا میگوییم در حالت 1 دوبار با قهرمان مسابقه میدهد، و خب احتمال برد قهرمان خیلی بیشتر از پسر است نسبت به برد پدر به پسر! بنابراین انتخاب مدل 2 برای سه ست بازی پسر معقول تر است تا برنده شود.
باز هم سناریو ها را با کد نویسی طراحی کردم،احتمال برد پدر از پسر را 50 درصد و احتمال برد قهرمان از پسر را 75 درصد فرض کردم. و سپس سناریوهای مدل اول و مدل دوم را طراحی کردم و  صد هزاربار این مدل ها را انجام و تکرار کردم؛ نتیجه باز اعجاب آور بود! برخلاف تصور شهودی ما، احتمال برد دو مسابقه پشت سر هم توسط پسر، در مدل اول یعنی قهرمان – پدر – قهرمان بیشتر بود! البته اینجا این اختلاف 3 درصد بود اما با تغییر احتمال بردها میشود اختلاف را چشم گیرتر نیز کرد؛ اما در هر صورت نتیجه بر خلاف تصور شهودی ما بود!

بازی سوم، مسئله مسابقه تلویزیونی(مسئله مونتی هال)

فرض کنید در یک مسابقه تلویزیونی شرکت کرده اید؛ در آخر مسابقه سه جعبه برای انتخاب دارید، یکی از آنها سکه طلا و دو جعبه دیگر محتوی چندین دلار هستند.
شما به اختیار یکی را انتخاب میکنید، سپس مجری از دو جعبه باقی مانده، یکی را که پوچ است(یا فقط محتوی چند دلار است) برای شما حذف میکند و به شما این فرصت را میدهد که انتخاب خود را عوض کنید یا بر سر انتخاب اول خود بمانید؛ شما کدام کار را انجام میدهید؟ بیایید در برنامه نویسی پایتون این مسئله را شبیه سازی کنیم:)

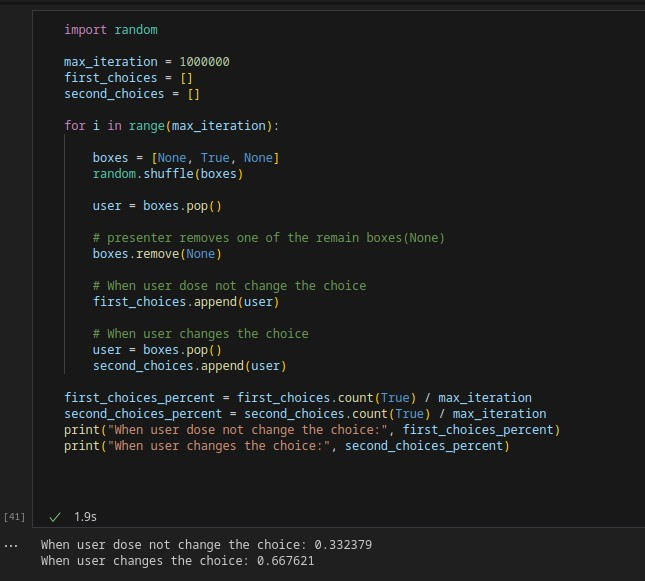
اگر بخواهم به طور خلاصه کدها را توضیح دهم، اینگونه است که مثل بازی های قبلی، بارها و بارها(استفاده از حلقه) مسابقه را با شرکت کنندکان متفاوت اجرا کرده ایم تا در نهایت نتیجه گیری قابل قبولی بدست آوریم؛ سپس یک لیست از سه جعبه تعریف کرده ام که یکی True یعنی دارای جایزه ارزشمند و دو تای دیگر None یا دارای جایزه کم ارزش یا پوچ است؛ سپس با متود شافل کتابخانه رندوم، آنها ها را بُر زده ام و سپس آخرین عنصر لیست را حذف کرده و در متغیر user ریخته ام؛ بنابراین کاربر یا شرکت کننده اولین انتخاب خود را میکند؛ سپس مجری یکی از دو جعبه باقی مانده را که پوچ باشد حذف میکند و بعد انتخاب های کاربر را در حالت های حفظ انتخاب اول یا تغییر انتخاب در دو لیست ذخیره کرده ایم؛ سپس تعداد True ها را شمرده و بر دفعات آزمایش تقسیم میکنیم؛ همانطور که میبینید، در حالتی که کاربر انتخاب خود را عوض کرده، 66 درصد احتمال برنده شدن دارد، اما در حالتی که بر سر انتخاب اول خود مانده، 33 درصد احتمال برد دارد.
الان پی بردم که دوران بچگی مسابقات تلویزیونی را میدیدم، چرا مجری شرکت کننده ها را به تغییر انتخاب تشویق میکرد! :)

صفحه ویکی پدیای مسئله مونتی هال

در کلاس یکی دو بازی دیگر نیز مطرح شد که جالب بودند؛ یکی از آنها این بود که استاد تعدادی کاغذ را در دست داشتند و از دانشجوها پرسیدند که این کاغذ ها چندتاست؛ هر دانشجو تعدادی مد نظر داشت، در نهایت با میانگین گیری از اعداد شهودی دانشجوها، میانگین بسیار به تعداد واقعی نزدیک تر بود!

دانلود سورس کدها(جوپیتر نوت بوک)

امیدوارم این مطلب براتون مفید بوده باشه:)